The Core of Attention is Communication

Over the past year, perhaps the most cited paper across the software industry is Attention is All You Need that is at the heart of ChatGPT and GPT transformer models. The first thing you will notice in the paper is the Attention formula:

\[\text{Attention(Q, K, V)} = \text{softmax}(\frac{QK^T}{\sqrt{d\_k}})V\]

Unfortunately, very few sources have delved into where this has come from i.e. the core of the attention mechanism, and most explanations provide little to no intuition. For example, the celebrated illustrated transformer says

What are the “query”, “key”, and “value” vectors?

They’re abstractions that are useful for calculating and thinking about attention. Once you proceed with reading how attention is calculated below, you’ll know pretty much all you need to know about the role each of these vectors plays.

Well, squinting my eyes here! That’s not enough for my taste. Now we are going to put ourselves in the mind of the authors of the paper and try to rediscover such formula.

Rediscovering Attention

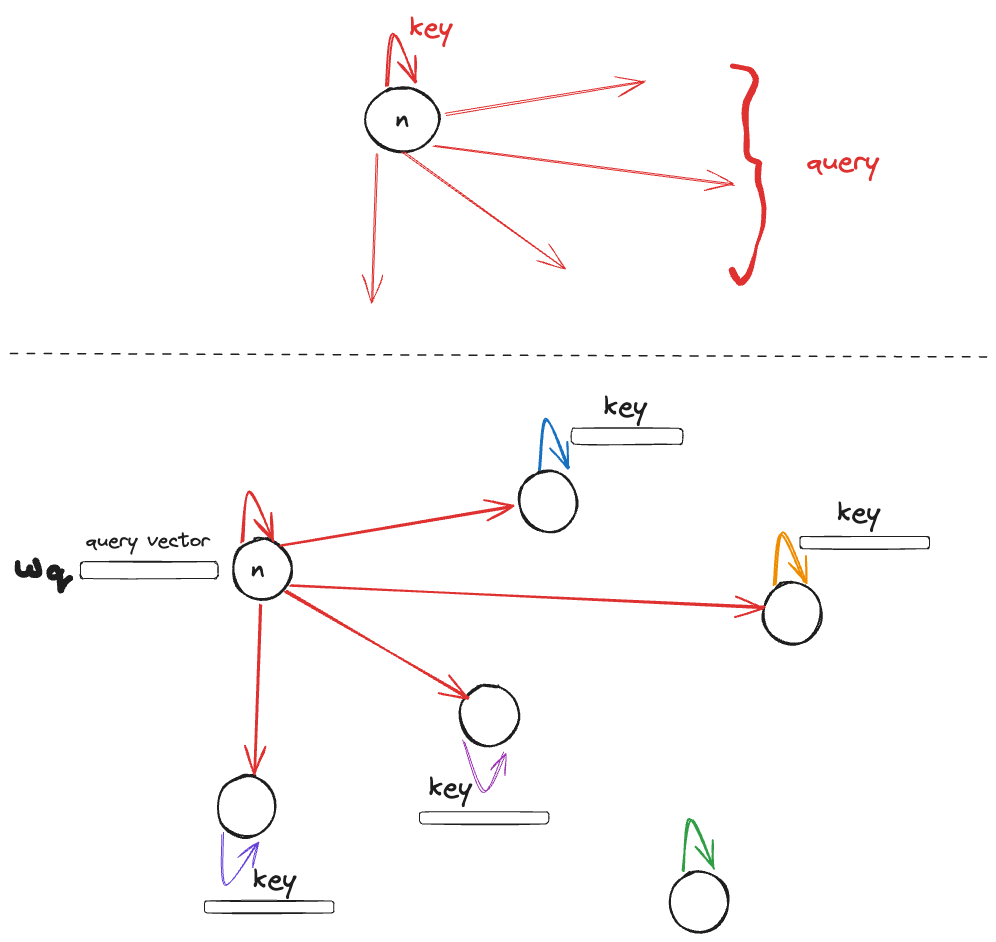
Interestingly, the of core attention hasnothingto do with Deep Learning.Attention is in fact a communication mechanism in a graph / network. Let me explain how. Given a directed graph \(G = (N, E)\), where \(N\) is the set of nodes and \(E\) a set of edges, we can associatetwopieces of information to each node \(n\);(key, query)where key is the “identity” of the node, query is what thenode is looking for and is interested in finding. (Note there is no value piece yet). Take the following directed graph. The red arrows from the view point of node \(n\). The key is the self-arrow and the rest of the arrows make up the query piece. We haven’t yet defined key and query.

We can parameterize key and query and represent them as (learnable) vectors (in PyTorch nn.Parameter). So now looking at other nodes key vectors, the node \(n\) can find its interest / “attention” score by for example computing cosine similarity (cosSim) between its query and the key of every other neighbours (connected to) i.e. \[\text{cosSim}(w\_q, \hat{w}\_k)\]

and gathering all the similarity scores in a vector

\[ \text{scores} = (\text{cosSim}(w\_q, \hat{w}\_1), \text{cosSim}(w\_q, \hat{w}\_2), ..., \text{cosSim}(w\_q, \hat{w}\_m))\]

So far so good! now what to do with this similarity vector? we need to include another piece which is thevalue. This value is the internal representation of nodes so for \(n\) let’s denote it by \(w\_v\) (note it’s parameterized to be learned). Normally, we would start with some value. For example in the NLP, node / token embedding and adjust that iteratively. But for now, we can assume the value vector is given so we update it by the discovered similarity scores for example by element-wise multiplication

\[\text{scores} \odot w\_v\]

Note it doesn’t have to be element-wise multiplication but that seems to be the simplest case here. Now, recall

\[\text{cosSim}(a, b) = \frac{ab^T}{\| a\| \| b \|}\]

so

\[\text{scores} = (\text{cosSim}(w\_q, \hat{w}\_1), \text{cosSim}(w\_q, \hat{w}\_2), ..., \text{cosSim}(w\_q, \hat{w}\_m))\]

isalmostequivalent to

\[\text{cosSim}(w\_q W\_k^T)\]

where \(W\_k\) is a matrix formed by stacked all keys in rows. Note here, we have to be careful about full vector-matrix multiplication because we need to only multiply \(w\_q\) to the keys of its neighbours. Let’s simplify and put that details aside. So as you can see the final rediscovered attention formula from the view point of a single node \(n\) is

\[\text{cosSim}(w\_q W\_k^T) w\_v\]

or putting the “weights” \(w\_\star\) down

\[\text{cosSim}(q K^T) v\]

and going for all nodes by stacking their vectors into matrices, we will get at

\[\text{cosSim}(QK^T) V\]

it’s not hard to see it resembles the original attention formula

\[\text{softmax}(\frac{QK^T}{\sqrt{d\_k}})V\]

dim = 64
w_q = nn.Parameter(torch.randn(dim))
W_k = nn.Parameter(torch.randn(dim, dim))
w_v = nn.Parameter(torch.randn(dim))
attention_scores = w_q @ W_k
attention_weights = F.softmax(attention_scores, dim=0)
output = attention_weights @ w_v

In fact, \(\text{cosSim}\) was replaced with \(\text{softmax}\) (and the additional \(\sqrt{d\_k}\) normalization). Also it turns out the \(\text{cosSim}\) version is calledContent-base attentionand is used in Neural Turing Machine. In fact, others have tried different “adjustments” to the formula as highlighted here.

How does this formulation map to graphs from NLP, CV etc?

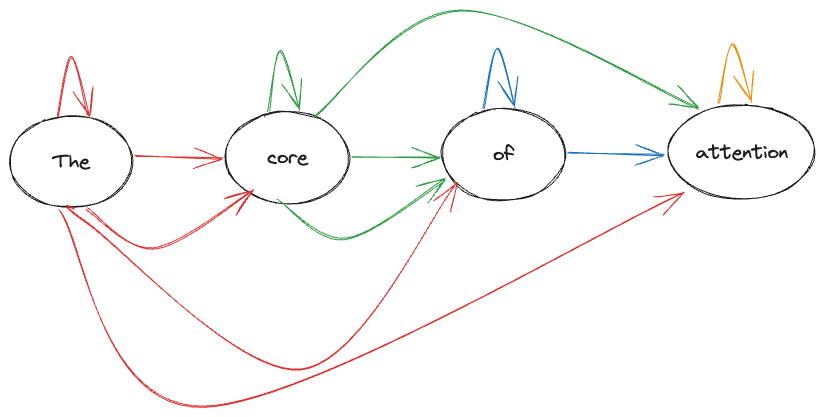
NLP and Vision make explicit use of it by creating the graph suitable for their tasks. For example, in (Causal) Language Model (LM) the core of (GPT) attention graph looks like

It is auto-regressive i.e. only past informations / edges are allowed so with a proper mask (lower-triangular matrix) we can zero out the future information

attention_scores = w_q @ W_k
tril = torch.tril(torch.ones(T, T)) # lower-triangle matrix of 1s
attention_scores = attention_scores.masked_fill(tril == 0, float('-inf')) # masks the future and set to -inf
attention_weights = F.softmax(attention_scores, dim=0)
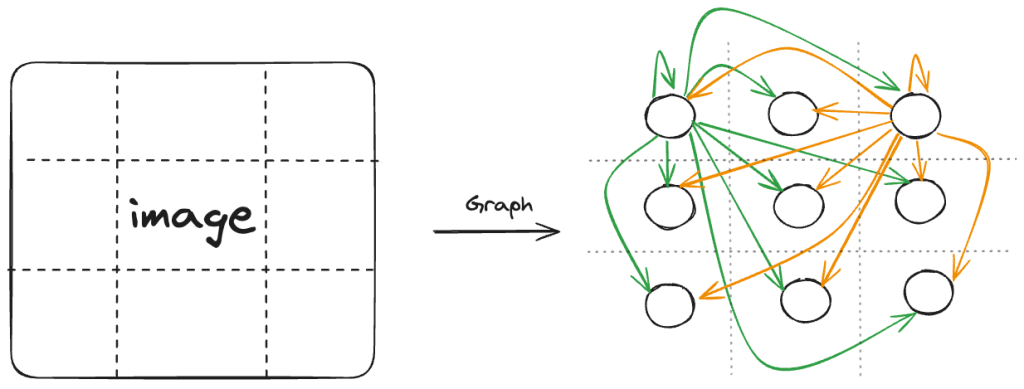
output = attention_weights @ w_v

Or in Vision, the attention graph of the vision transformer model (ViT) from An Image is Worth 16 x 16 Words looks like this (complete graph i.e. all nodes are connected to each other)

Summary

We tried to rediscover the attention formula and did it by putting the attention in a higher context i.e.communication in a graph. Note that depending on the task and the graph at hand we need to make adjustments like in the LM case, by masking out future information. Also the general notion of Attention has no notion of position and that is why encoding and incorporating positions i.e. positional encoding in LM is important. The complexity grows from here and we can create Multi-Head Attention and even more general Cross-Attention (with encoder-decoder). But these are less important than the core intuition I wanted to give in this post. Hope this post has clarified attention and the intuition behind it. If you are interested in more detail implementation of the Attention-is-all-You-Need paper, I recommend checking out annotated implementation in labml.